Table of Contents
The refocus Gimp plug-in can be used to sharpen images. Frequently, when processing images, e.g. when scanning photo's or slides, the images become slightly blurred. This plug-in attempts to "refocus" the image. In many cases this plug-in produces much better results than similar plug-ins such as sharpen or unsharp mask.
This plug-in has a preview that helps you select the best parameters.
Instructions for installing the plug-in are described in Installation.
Instructions for using the plug-in are described in Using the plug-in.
The home page for the Refocus plug-in is located at http://refocus.sourceforge.net.
For installing refocus you need the following:
The Gimp, of course. This plug-in should work with versions > 1.2.
Gtk+-2 plus pkg-config.
Optional: ATLAS, see Using ATLAS
Installation should be simple. Untar the distribution. If you want to use ATLAS install it in lib-atlas (see Using ATLAS).
Then run ./configure in the top-level directory.
Then run make install-bin if you want to install the plug-in under your home directory or make install-admin-bin if you want to install the plug-in under your Gimp's system directory.
If you have gtk-doc installed you can build the system documentation in the gtk-doc directory. In this case you must invoke configure with the --enable-gtk-doc option. When you make it for the first time make will fail with the message No rule to make target `tmpl/*.sgml'. Running make again will fix this problem.
ATLAS (see http://math-atlas.sourceforge.net) is a system for generating high-performance mathematical libraries. It generates a library that is specifically tuned to your processor and compiler. refocus needs some routines for solving a linear system of equations. By default refocus uses an unoptimized version from the CLAPACK distribution (see http://www.netlib.org/clapack/).
Make ATLAS generate its libraries. For instructions see the ATLAS documentation. Depending on your system, this may take a long time. During the installation you have to select a name to identify your configuration. In the following examples we will use Linux_PII as the chosen name.
Go to the subdirectory lib/Linux_PII and run make.
cd lib/Linux_PII make
This will generate a gzipped tar file that contains the generated libraries and include files.
Copy the gzipped tar file to the refocus directory and unpack it.
cp ~/ATLAS/lib/atlas3.4.1_Linux_PII.tgz ~/refocus cd ~/refocus zcat atlas3.4.1_Linux_PII.tgz |tar xvf - mv Linux_PII lib-atlas
If you have already run configure , you must delete the file config.cache.
Then run configure. If everything is OK you should see a message like using atlas in lib-atlas/lib.
Now run make.
You can start the plug-in by clicking with the right mouse-button in the image, and then select from the Filters menu Enhance/Refocus.
The plug-in window looks something like this:
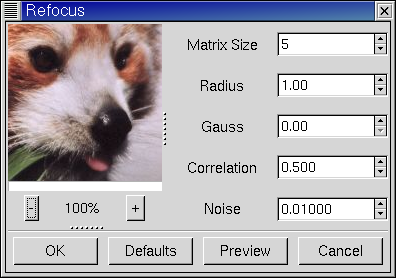
The plug-in window contains a preview of the image on the left and on the right a set of spin-buttons to change its parameters.
The bottom of the preview contains the following buttons:
- OK
Quit the plug-in and apply the selected transformation to the image.
- Defaults
Select default values for all parameters.
- Preview
Compute the new transformation matrix and show the results in the preview. Because computing the transformation matrix can take a lot of time, it is not automatically recomputed, when the parameters in the spin-buttons have changed. When you have changed parameters the Preview button will change to active, i.e. it is no longer grayed out.
Warning
When the plug-in starts it shows the original untransformed image. When you press the Preview button the transformation matrix is computed and the transformed image will be shown in the preview.
- Cancel
Quit the plug-in without applying the selected transformation to the image.
The preview allows you to preview the output of the plug-in.
You can scroll the preview by pressing the first mouse-button and dragging in the preview. During scrolling, the original unprocessed image will be shown, because the plug-in is not fast enough to compute the processed image. When you release the mouse-button the plug-in will start computing the processed image. Immediately below the preview is a progress-bar that shows the plug-in's progress.
You can scale (or zoom) the image with the + and - buttons under the preview. When you zoom out the plug-in has to render a larger area which takes more time.
The size of the preview can be changed by dragging the paned widgets below and to the right of the preview. These widgets are marked with "....".
The plug-in has the following parameters:
- Matrix Width
This parameter determines the size of the transformation matrix. Increasing the Matrix Width may give better results, especially when you have chosen large values for Radius or Gauss. Note that the plug-in will become very slow when you select large values for this parameter. In most cases you should select a value in the range 3-10.
- Radius
This is the Radius of the circular convolution. This is probably the most important parameter for using the plug-in. For normal images, the default value of 1 should give good results. Select a higher value when your image is very blurred.
- Gauss
This is the radius for the Gaussian convolution. Use this parameter when you blurring is Gaussian. In most cases you should set this parameter to 0, because it causes nasty artifacts. When you use non-zero values you will probably have to increase the Correlation and/or Noise parameters, too.
- Correlation
Increasing the Correlation may help reducing artifacts. The correlation can range from 0-1. Useful values are 0.5 and values close to 1, e.g. 0.95 and 0.99. Using a high value for the correlation will reduce the sharpening effect of the plug-in.
- Noise
Increasing the Noise parameter may help reducing artifacts. The Noise can range from 0-1. When the Noise value is to low, e.g. 0 the image quality will be horrible. A useful value is 0.01. Using a high value for the Noise will reduce the sharpening effect of the plug-in.
This section describes a few hints to help you work with the refocus plug-in.
Perform all color corrections on the image before using this plug-in.
In many cases you should use this plug-in before performing other operations on the image. The reason is that many operations on the image will leave boundaries that are not immediately visible but that will leave nasty artifacts.
When you are scanning images and compress them, e.g. to jpg, you should use the plug-in on the uncompressed image.
The performance of the plug-in when you are previewing depends heavily on the Matrix Width, the size of the preview and the scale of the preview.
The execution time for transforming the image depends quadratically on the Matrix Width. So when you double the Matrix Width, it takes four times as long to process the image. Values in the range of 3-8 usually give good results.
The plug-in has to transform the entire part of the image that is shown in the preview. Using a smaller preview and/or a larger scale will improve the plug-in's performance.
The time needed for computing the transformation matrix after you have pressed the Update button depends dramatically on the Matrix Width. Using a smaller value for Matrix Width will give you much better performance for this part of the computations. You should also consider using ATLAS (see Using ATLAS).
A wide range of image transformations can be described mathematically as convolutions. A convolution is a linear transformation where each destination pixel is the weighted sum of the pixels in the neighborhood of the original pixel.
For example, the following matrix describes the convolution where each pixel is the average of the source pixel and its 8 immediate neighbors:
| 1/9 | 1/9 | 1/9 |
| 1/9 | 1/9 | 1/9 |
| 1/9 | 1/9 | 1/9 |
A wide range of image degradations, e.g. bad focusing and motion blur, can adequately be described with convolutions.
In this case we are interested in undo-ing the effect of a convolution. Using Fourier analysis it is possible to show that for each convolution there exists an inverse convolution.
Unfortunately, this inverse convolution is of little practical use. The reason is that image transformations virtually always introduce some form of error, e.g. due to noise in the scanner or simply round-off errors. The unmodified inverse convolution greatly amplifies these errors. In many cases the result of the inverse convolution is completely dominated by the noise. If you want to get a feeling what this means, run the plug-in with Gauss = 2 and Correlation and Noise = 0.
A standard solution is to use Wiener filtering. Wiener filtering finds an inverse convolution that attempts to minimize noise. Normally Wiener filtering is implemented with Fourier transforms.
Standard Wiener filters have two disadvantages for our purpose:
The memory requirements are high.The Fourier transform of the image requires two floating point numbers for each pixel.
Wiener filtering is a global transform. The results for a specific region can be influenced by completely unrelated regions in the image. During experiments with Wiener filtering I found that this frequently produces unexpected and undesirable results.
The refocus plug-in is based on a modified form of the Wiener filter, called the FIR (Finite Input Response) Wiener filter. A FIR Wiener filter only uses a limited neighborhood of the source pixels and can be easily implemented as a convolution matrix.
FIR Wiener filtering has the following advantages:
Low memory requirements. Only the convolution matrix must be stored.
Ease of implementation. There is no need to do a full Fourier transform.
The transformation is local. The results only depend on a small neighborhood of the original pixel.
For technical background on the FIR Wiener deconvolution see [Jain89].
In most cases you don't know precisely what convolution caused the image degradation. There are two convolutions that are frequently used to model image degradation:
The Gaussian convolution
The Circular convolution
The Gaussian convolution is mathematically similar to the normal distribution, with its bell-shaped curve. From a theoretical point of view the mathematical justification for using the Gaussian convolution is that when you a apply a large number of independent random convolutions the results will always approach a Gaussian convolution.
The circular convolution spreads each source point uniformly across a small disk with a fixed radius. Technically this describes the effects of using a (ideal) lens that is not correctly focused.
The refocus plug-in supports both the Gaussian and the circular convolution plus mixtures of both.
The Radius parameter determines the radius of the circular convolution. The Gauss parameter determines the width of Gaussian convolution.
The actual convolution that is used by the plug-in is in fact the result of convolving both the Gaussian and the circular convolution with one another. Both of these convolutions are identical to the identity convolution when their parameter is equal to 0. Therefore, when the Gauss parameter equals 0, the result is a circular convolution, and likewise when the Radius equals 0 the result is a Gaussian convolution.
In practice, I found that in most cases the circular convolution works much better than the Gaussian convolution. The Gaussian convolution has a very long tail, so mathematically the result of the convolution also depends on source pixels at a large distance from the original source pixel. The FIR Wiener inverse of a Gaussian convolution in most cases is heavily influenced by source pixels at a large distances, and in most cases this produces undesirable results.
The circular convolution generally produces much better results. One reason is that the FIR Wiener inverse of the circular convolution in general influenced by source pixels in the immediate neighborhood of the original source pixel. Another reason is that a circular convolution is theoretically a good mathematical model for images that are slightly unfocused.
Two other techniques that are frequently used to enhance images are:
Sharpening
Unsharp mask
Sharpening applies a small convolution matrix that increases the difference between a source pixel and its immediate neighbors. FIR Wiener filtering is a more general technique because it allows a much larger neighborhood and better parameterizations. Sharpening only works when your images are very slightly blurred. Furthermore, for high values of the sharpening parameter the results frequently look "noisy". With FIR Wiener filtering this noise can be greatly reduced by selecting higher values for the Correlation and Noise parameters.
Unsharp masking is another very popular image enhancement technique. From a mathematical point of view its justification is a bit obscure but many people are very fond of it. The first step is to blur the source image, hence the name unsharp masking. Then the difference between the source image and the blurred image is subtracted from the source image.
In general, unsharp masking produces better results than sharpening. This is probably caused by the fact that unsharp masking uses a larger neighborhood than sharpening.
From a theoretical point of view unsharp masking must always introduce artifacts. Even under optimal circumstances it can never completely undo the effect of blurring. For Wiener filtering it is possible to prove that it is the optimal linear filter.
In practice I found that in virtually all cases the results of the FIR Wiener filter were at least as good as those of unsharp masking. The FIR Wiener filter is frequently better in restoring small details.
As a side note, unsharp masking generally uses a Gaussian convolution, I suspect that in some cases a circular convolution should give better results.